Makaleler

Matematiğin Milyon Dolarlık Problemleri

Merve Atasever

09-12-2015 09:42
249843 kez okundu.

Matematiğin Milyon Dolarlık Problemleri — Bir matematik sorusu ne kadar zor olabilir ki şimdiye dek çözülemesin? Bazen tek satırlık, basit gibi görülen problemlerin sayfalarca çözümü veya ispatı olabiliyor. Her biri için 1 milyon dolar ödül koyulmuş sorulardan 6 tanesi için henüz tam ispatlar bilinmiyor.

21. yüzyılda hala çözülememiş matematik soruları olması lisans eğitimine bu alanda devam etmemiş insanlara ilginç gelecektir. Bir matematik sorusu ne kadar zor olabilir ki şimdiye dek çözülemesin? Bazen tek satırlık, basit gibi görülen problemlerin sayfalarca çözümü veya ispatı olabiliyor. “Open problems” dediğimiz, henüz çözümü bilinmeyen soruların çoğunu, sadece anlayabilmek için bile topoloji, modern cebir, sayılar teorisi gibi matematiğin temel dallarında belli bir birikim gerekiyor. Bu sorulardan en ünlüleri Alman matematikçi David Hilbert’in 1900’de yayınladığı 23 tane sorusu ve Clay Matematik Enstitüsü’nün ödüllü 7 sorusudur. (Millennium Prize Problems) Her biri için 1 milyon dolar ödül koyulmuş sorulardan 6 tanesi için henüz tam ispatlar bilinmiyor.

Bu sorulardan biri olan Poincaré sanısı geçtiğimiz yıllarda Rus matematikçi Grigori Parelman tarafından çözüldü. Soru, 1904’te Fransız matematikçi Henri Poincaré ortaya attığından beri topolojinin önemli bir bilinmeziydi. (Topoloji kelime olarak farklı çağrışımlar yapıyor ama matematiğin cisim geometrilerini inceleyen dalı aslında.) Bir küre (3 boyutlu uzayda 2 boyutlu yüzey) düşünelim. Bu kürenin etrafındaki herhangi bir halkayı yüzeyi delmeden ya da yüzeyden ayrılmadan tek bir noktaya büzebiliriz; yani küreyi basit bağlantılı (deliği olmayan) bir çokkatlı olarak görebiliriz.

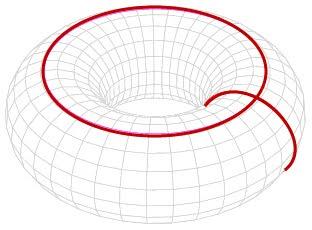
Mesela aynı şeyi donut için söyleyemeyiz. Şekildeki kırmızı halkaları tek bir noktaya büzebilmek için yüzeyi delmek veya yüzeyden ayrılmak gerekiyor.

Poincaré bu özelliği kullanarak 3 boyutlu uzayda küreyi karakterize etmiş ve yüksek boyutlar için de bu özelliğin geçerli olduğunu iddia etmiştir. Yani içinde her çemberin bir noktaya büzülebildiği kenarsız ve tıkız bir uzayın, 4 boyutlu Öklit uzayında yatan 3 boyutlu bir küre olması gerektiğini söylemiştir. Yaklaşık 100 yıl sonra Parelman konjektürü ispatlamış ama enstitünün para ödülünü ve geometrik topoloji alanındaki çalışmalarından ötürü kazandığı matematiğin Nobel’i kabul edilen Fields madalyasını ( International Mathematical Union tarafından 40 yaş altı matematikçilere verilen çok prestijli bir ödül) almayı reddetmiştir. Bu pek de olağan olmayan haber ilk duyulduğunda ben liseye gidiyordum ve adamın ormanda mantar toplamaktan hoşlanan enteresan biri olduğunu okumuştum.

Open problems için sayılar teorisinden bir örnek vereyim; tek mükemmel sayılar var mı? Kendisi hariç pozitif tam sayı bölenlerinin toplamına eşit sayılara mükemmel diyoruz. Mesela 6’yı ele alalım; 1,2 ve 3 tarafından bölünebiliyor ve 1+2+3=6 , yani 6 bir mükemmel sayı. Çift mükemmel sayıların formlarıyla ilgili bir şeyler biliyoruz. Örneğin, p’yi Mersenne asalı (2^n - 1 formunda yazılabilen asal sayılar) aldığımızda p(p+1)/2 bize her zaman bir çift mükemmel sayı veriyor. (Euclid-Euler Teoremi) Fakat tek sayılarda mükemmel sayı olup olmadığı ya da sonsuz çoklukta mükemmel sayı olup olmadığı henüz bilinmiyor.

Sayılar teorisinden devam edecek olursam, sonsuz sayıda ikiz asal ( p ve p+2 ikilisinin asal olması) var mı sorusunun ispatı da henüz bulunabilmiş değil. Buna benzer asal sayıları belli formlara sokma, bunların sonlu ya da sonsuz sayıda olması ve aynı formdaki asal sayıların aralarındaki farkın gittikçe açılıp açılmayacağıyla ilgili çözülememiş çok sayıda soru mevcut. (asal sayılarla ilgili çalışmalar kriptolojide de çokça kullanılıyor) Matematikçiler bu alanlardaki çalışmalarını sürdürmeye devam ediyor. Boğaziçi Üniversitesi matematik bölümü hocalarından Prof. Dr. Cem Yalçın Yıldırım’da ikiz asal sayıların dağılımı üzerine yaptığı çalışmalardan dolayı 2014 yılında American Mathematical Society tarafından Frank Nelson Cole Prize ile ödüllendirilmiştir.

Soyut bilimlerin güzelliği sonsuz olmalarında yatıyor. Matematik ne kadar ilerlerse o kadar çok yeni soru getiriyor beraberinde. Örneklendirdiğim gibi hala asırlık çözülemeyen sorular var. Bazen bu alanda çalışmayan insanlar çözümlere dair iddialarda bulunup popüler televizyon programlarına haber oluyorlar. Tabi ki bu işler o kadar kolay değil, belli bir birikim ve zaman harcama gerektiriyor. Bu kadar çok bilinmeyenin olduğu bir dünyada çalışırken hepimize kolay gelsin.

Detaylı okuma için
http://mathworld.wolfram.com/UnsolvedProblems.html
http://www.claymath.org/millennium-problems/poincar%C3%A9-conjecture
http://www.clarku.edu/~djoyce/hilbert/

Görsel Kaynaklar
https://prateekvjoshi.files.wordpress.com/2013/02/rubber-band-and-sphere.jpg
http://3.bp.blogspot.com/_3cvpfoj7mb8/TGLjBZIhLqI/AAAAAAAACrA/Co4zJinD8MA/s1600/conjecture2.jpg
http://experimentalmath.info/blog/wp-content/uploads/2013/05/shrn706l.png